1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
角柱の体積の求め方は、公式に当てはめるのが一番簡単です! 角柱の体積 = 底面積× 高さ 角 柱 の 体 積 = 底 面 積 × 高 さ この公式で求めることができます。 では問題を1問解いて円柱の体積、表面積の求め方はこれでバッチリ! ←今回の記事 円錐の表面積、中心角の求め方を解説! 裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式は
円柱 の 面積 の 求め 方
円柱 の 面積 の 求め 方- この円柱は半径7cmの円が底面、高さが12cmなので 円柱の体積=7×7×314×12=(cm³)となります。 答え 円柱ができる。 体積はcm³ ~立 ホールの面積が大きくなれば、相対的に壁面の面積の合計値は小さくなります。」 と書かれてますが、 容積に比例して壁面の面積の合計値も増えるのではないのですか? アホな質問
円柱の表面積 計算が簡単にできる電卓サイト
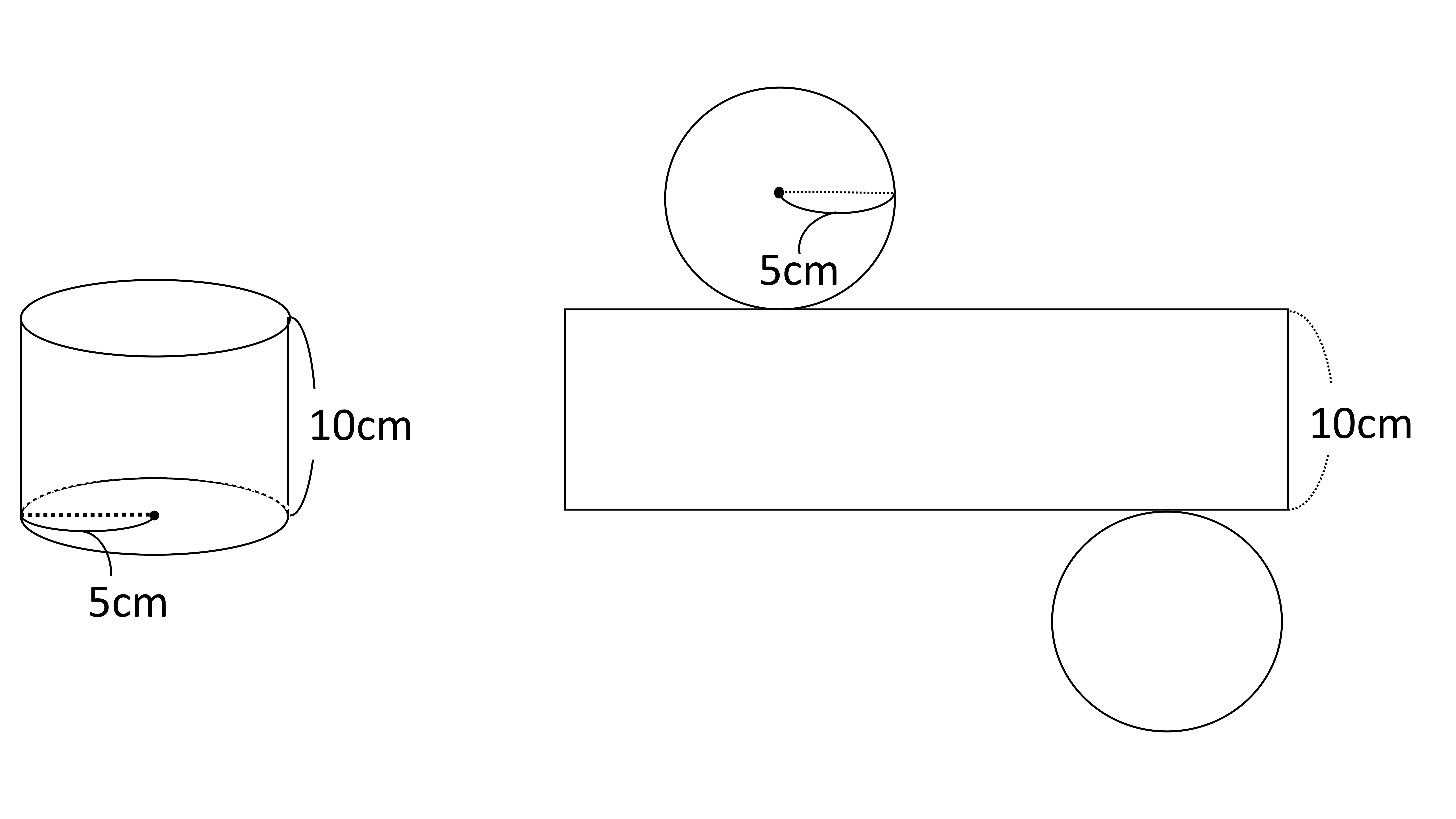
ここで、S は円の面積、π は円周率、r は円の半径を表します。 このページの続きでは、この公式の導き方のイメージと、円の面積を求める計算問題の解き方を説明しています。 小学生向けに文字を 円柱の表面積の求め方を3ステップで解説していくよ。 3ステップでわかる!円柱の表面積の求め方 例題をときながら円柱の表面積の求め方を勉強していこう。 例題 半径3cm、高円柱の容積の求め方は、円の半径×半径×円周率×高さです。 これは表面積×高さを計算しています。 円と四角形では表面積が違いますが、根本の計算は、立方体や直方体の式と同じです。 今回は円
直円柱の半径と高さから体積、側面積 、表 円柱状の入れ物に入っている小粒の物を、四角い入れ物に入れ替えようと考えておりました 法務系の事務方なのに材料費の計算をすることになってし
円柱 の 面積 の 求め 方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「円柱 の 面積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円柱 の 面積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「円柱 の 面積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「円柱 の 面積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「円柱 の 面積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「円柱 の 面積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円柱 の 面積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円柱 の 面積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円柱 の 面積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「円柱 の 面積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「円柱 の 面積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |





0 件のコメント:
コメントを投稿